引言 #
本文分享第一个机器学习算法：K-近邻算法（K-Nearest Neighbor, KNN），最初由Cover和Hart于1968年提出，是最简单的机器学习算法之一。我将从以下几个方面对K-近邻算法进行分享：首先，我将分享K-近邻算法的基本理论概念；其次，我将使用Python实现一个实战案例；最后，我将分享一些K-近邻算法常见的面试问题。
算法概述 #
你是否玩过二十个问题的游戏，游戏的规则很简单：参与游戏的一方在脑海里想某个事物，其他参与者向他提问问题，只允许提问20个问题，问题的答案也只能用对或错回答。问问题的人通过推断分解，逐步缩小待猜测事物的范围。
决策树的工作原理与20个问题类似，用户输入一系列数据，然后给出游戏的答案。如下图所示是一个决策树的流程图。图中构造了一个假想的邮件分类系统，它首先检测发送邮件域名地址。如果地址为“myEmployer.com”，则将其放在分类“无聊时需要阅读的邮件”中。如果邮件不是来自这个域名，则检查邮件的内容是否包含单词“曲棍球”，如果包含则将邮件归类到“需要及时处理的朋友邮件”，如果不包含则将邮件归类到“无需阅读的垃圾邮件”。
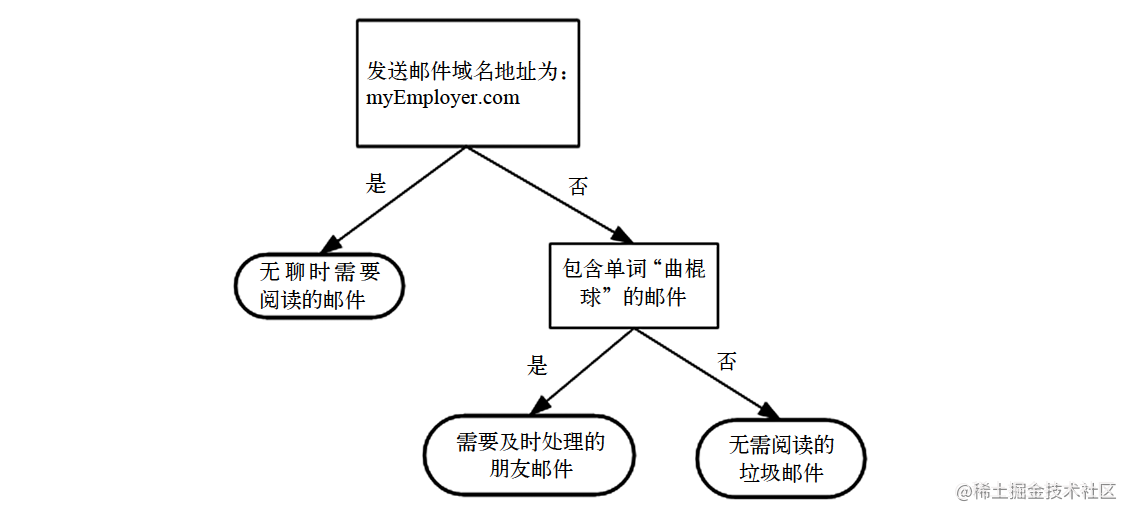
决策树算法的预测分类流程如下：
- 特征选择。在构建决策树时，首先需要选择用于分裂节点的最佳特征。常用的特征选择方法有信息增益、信息增益比、基尼指数等。这些方法根据特征的不确定性或纯度来衡量特征的重要性。
- 分裂节点。根据选择的特征，将节点分裂成多个子节点。每个子节点代表一个特征取值，将数据集按照该特征取值进行划分。
- 递归构建。对于每个子节点，重复执行特征选择和分裂节点的过程，直至满足停止的条件。停止的条件可以是达到最大深度、节点中的数据样本小于预定义阈值或节点的不确定性或纯度低于阈值等。
- 标记叶子节点。当达到停止条件时，将叶子节点标记为特定的类别标签或预测值。对于分类问题，叶子节点通常表示一个类别。（对于回归问题，叶子节点表示一个数值）
- 预测。通过将输入样本从根节点开始沿着决策树的路径进行遍历，最终达到叶子节点，从而预测样本的类别。（或数值）
决策树算法的优缺点如下：
优点：
- 可解释性强。决策树的结构清晰，易于理解和解释。可以通过可视化展示决策树，直观地观察到决策过程和特征的重要性。
- 处理混合数据类型。决策树可以处理包含离散型和连续型特征的数据，而无需对特征进行特殊的预处理或转换。
- 对缺失值和异常值鲁棒。决策树能够自然地处理缺失值，并且对异常值相对鲁棒，不会对异常值过度敏感。
- 计算效率高。相对于其他复杂的机器学习算法，决策树的训练和预测速度较快，尤其适用于处理大型数据集。
缺点：
- 容易过拟合。决策树容易生成过于复杂的模型，过拟合训练数据，导致在新数据上的泛化能力较差。可以通过剪枝等方法来减轻过拟合问题。
- 忽略特征间的相关性。决策树基于每个节点上的最佳特征进行分裂，可能忽略特征之间的相关性。在某些情况下，其他算法（如基于统计的方法）能够更好地处理特征之间的复杂关系。
- 对噪声敏感。当数据中存在噪声时，决策树可能会过度拟合噪声，导致模型不稳定。
实战案例 #
案例概述 #
本文使用一组海洋生物数据，需要将这些动物分为两类：鱼类和非鱼类。如下表所示的数据包含5个海洋动物，特征包括：不浮出水面是否可以生存，以及是否有脚蹼。现在需要决定是依据第一个特征还是第二个特征划分数据。本文将使用ID3算法划分数据集，该算法处理如何划分数据集，何时停止划分数据集。
信息增益 #
划分数据集的大原则是将无序的数据变得更加有序。组织杂乱无章数据的一种方法就是使用信息论度量信息，信息论是量化处理信息的分支科学。我们可以在划分数据之前或之后使用信息论量化度量信息的内容。在划分数据集之前之后信息发生的变化称为信息增益，知道如何计算信息增益，我们就可以计算每个特征值划分数据集获得的信息增益，获得信息增益最高的特征就是最好的选择。
集合信息的度量方式称为香农熵或者简称为熵，这个名字来源于信息论之父克劳德·香农。
熵定义为信息的期望值，在明晰这个概念之前，我们必须知道信息的定义。如果待分类的事物可能划分在多个分类之中，则符号$x_i$的信息定义为$l(x_i)=-log_2 p(x_i)$，其中，$p(x_i)$是选择该分类的概率。
为了计算熵，我们需要计算所有类别所有可能值包含的信息期望值，通过以下的公式得到：
$$H=-\sum_{i=1}^{n}p(x_i)log_2 p(x_i)$$
其中，n是分类的数目。
以下是基于Python实现的计算信息熵的代码：
from math import log
def calc_shannon_ent(dataset):
"""
Calculate Shannon Entropy of a dataset
"""
num_entries = len(dataset) # number of entries
label_counts = {} # dictionary to store the number of each class
# loop over all the entries
for feat_vec in dataset:
current_label = feat_vec[-1] # get the label of the current entry
if current_label not in label_counts.keys():
label_counts[current_label] = 0
label_counts[current_label] += 1 # increment the count of the label
shannon_ent = 0.0 # initialize Shannon Entropy
for key in label_counts:
prob = float(label_counts[key]) / num_entries
shannon_ent -= prob * log(prob, 2) # calculate Shannon Entropy
return shannon_ent
def create_dataset():
"""
Create a dataset
"""
dataset = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing', 'flippers'] # feature labels
return dataset, labels
在得到熵之后，我们就可以按照获取最大信息增益的方法划分数据集。
划分数据集 #
分类算法除了需要测量信息熵，还需要划分数据集，度量划分数据集的熵，以便判断当前是否正确地划分了数据集。我们将对每个特征划分数据集的结果计算一次信息熵，然后判断按照哪个特征划分数据集是最好的划分方式。以下是基于Python实现的数据集划分代码：
def split_dataset(dataset, axis, value):
"""
Split a dataset
"""
ret_dataset = []
for feat_vec in dataset:
if feat_vec[axis] == value:
reduced_feat_vec = feat_vec[:axis]
reduced_feat_vec.extend(feat_vec[axis+1:])
ret_dataset.append(reduced_feat_vec)
return ret_dataset
接下来我们将遍历整个数据集，循环计算香农熵和split_dataset()函数，找到最好的特征划分方式。熵计算将会告诉我们如何划分数据集是最好的数据组织方式。以下是Python实现的代码：
def choose_best_feature_to_split(dataset):
"""
Choose the best feature to split the dataset
"""
num_features = len(dataset[0]) - 1 # number of features
base_entropy = calc_shannon_ent(dataset) # base entropy
best_info_gain = 0.0 # initialize the best information gain
for i in range(num_features):
feat_list = [example[i] for example in dataset]
unique_vals = set(feat_list) # get the unique values of the feature
new_entropy = 0.0 # initialize the new entropy
for value in unique_vals:
sub_dataset = split_dataset(dataset, i, value)
prob = len(sub_dataset) / float(len(dataset))
new_entropy += prob * calc_shannon_ent(sub_dataset)
info_gain = base_entropy - new_entropy # calculate the information gain
if info_gain > best_info_gain:
best_info_gain = info_gain
best_feature = i
return best_feature
代码运行结果显示，第0个特征是最好的用于划分数据集的特征。
递归构建决策树 #
目前我们已经实现了从数据集构造决策树算法所需的子功能模块，其工作原理如下：得到原始数据集，然后基于最好的属性值划分数据集，由于特征值可能多余两个，因此可能存在大于两个分支的数据集划分。第一次划分之后，数据将被向下传递到树分支的下一个节点，在这个节点上，我们可以再次划分数据。因此可以采用递归的原则处理数据集。
递归结束的条件是：程序遍历完所有划分数据集的属性，或者每个分支下的所有实例都具有相同的分类。如果所有实例都具有相同的分类，则得到一个叶子节点或终止块。任何到达叶子节点的数据必然属于叶子节点的分类。以下是Python实现的代码：
def create_tree(dataset, labels):
"""
Create a decision tree
"""
class_list = [example[-1] for example in dataset]
if class_list.count(class_list[0]) == len(class_list):
return class_list[0]
if len(dataset[0]) == 1:
return majority_cnt(class_list)
best_feature = choose_best_feature_to_split(dataset)
best_feature_label = labels[best_feature]
my_tree = {best_feature_label: {}}
del(labels[best_feature])
feat_values = [example[best_feature] for example in dataset]
unique_vals = set(feat_values)
for value in unique_vals:
sub_labels = labels[:]
my_tree[best_feature_label][value] = create_tree(split_dataset(dataset,
best_feature,
value),
sub_labels)
return my_tree
面试问题 #
- 决策树算法的基本原理？ > 参考答案 > > 决策树是一种监督学习算法，用于分类和回归问题。它通过递归地划分数据集，选择最佳特征来构建树，并在叶节点做出预测。优点是简单易懂，能处理离散和连续特征，然而可能会过拟合。解决方法包括剪枝和使用集成算法。决策树的工作原理是以信息熵或基尼系数衡量特征选择，通过选择最佳特征划分数据集构建子树，递归过程一直持续到达到停止条件。预测时，根据特征值遍历树，得出了决策结果。决策树适用于解释性要求较高的问题，但对于复杂问题可能需要更复杂的模型。
- 如何选择决策树分割点？ > 参考答案 > > 在决策树算法中，选择最佳的分割点是一个关键的步骤，它决定了如何将数据集划分为更小的子集。选择分割点的目标是尽可能地降低子集的不纯度，使得每个子集内的样本属于同一类别或者回归得更好。在分类问题中，常用的准则有信息熵和基尼系数。对于回归问题，则通常使用平方误差或平均绝对误差作为准则。通过计算这些指标，我们可以找到最优的特征和阈值来进行分割。
- 什么是信息熵（Entropy）和基尼系数（Gini Impurity）？它们在决策树中有什么作用？ > 参考答案 > > 信息熵（Entropy）是信息论中的概念，用于衡量系统的不确定性或混乱程度。在决策树中，对于一个数据集D，其信息熵表示为H(D)，计算公式如下：\(H(D) = -\sum_{i=1}^{c} p_i \log_2(p_i) > \)。其中，c是数据集D中不同类别的数量，\(pi\)是数据集D中数据第i类的样本所占比例。信息熵越高，表示数据集越混乱，不确定性越大。 > > 基尼系数（Gini Impurity）是一种用于衡量数据集纯度的指标，在决策树中也常用于特征选择。对于一个数据集D，其基尼系数表示为Gini(D)，计算公式如下：\(Gini(D) = 1 - \sum{i=1}^{c} p_i^2\)。其中，c是数据集D中不同类别的数量，\(p_i\)是数据集D中属于第i类的样本所占比例。基尼系数越小，表示数据集的纯度越高。
如何解决决策树容易过拟合的问题？ > 决策树容易过拟合的问题是由于其对训练数据过度拟合的特性造成的。过拟合意味着决策树在训练数据上表现很好，但在未见过的测试数据上表现较差。为了解决决策树过拟合的问题，可以采取以下策略： > （1）剪枝（Pruning）：剪枝是一种通过裁剪决策树的部分分支来降低复杂性的方法。剪枝过程中，可以设定一个阈值或复杂度参数，决定是否对节点进行剪枝。剪枝能够减少树的深度和叶节点数量，从而降低过拟合的风险。（2）设置最小样本数和最大深度：通过限制每个叶节点的最小样本数和限制树的最大深度，可以防止决策树在训练数据中过度细分，减少过拟合的可能性。（3）使用交叉验证：使用交叉验证技术来评估模型性能。通过将数据集分为训练集和验证集，多次训练并评估模型，可以获得更准确的模型性能评估，避免过拟合。（4）随机森林（Random Forest）：随机森林是一种集成学习方法，它通过同时构建多棵决策树并进行组合预测，能够降低过拟合的风险，提高模型的泛化能力。（5）特征选择：选择更具代表性的特征能够帮助减少过拟合。可以使用特征选择技术，例如信息增益、方差选择等，来筛选重要的特征。
参考文献 #
[1] Harrington, P. (2012). Machine Learning in Action. Shelter Islan d, NY: Manning Publications.
最后一次修改于 2024-10-24